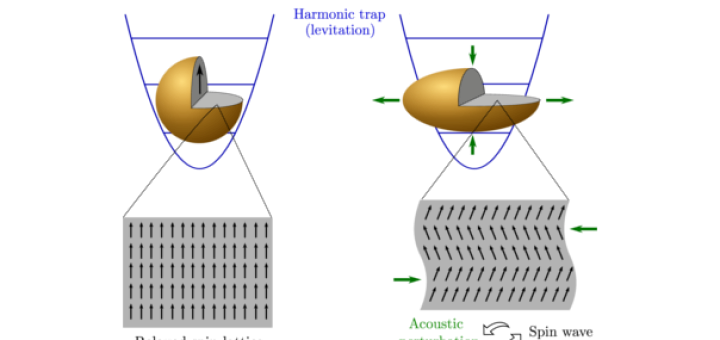
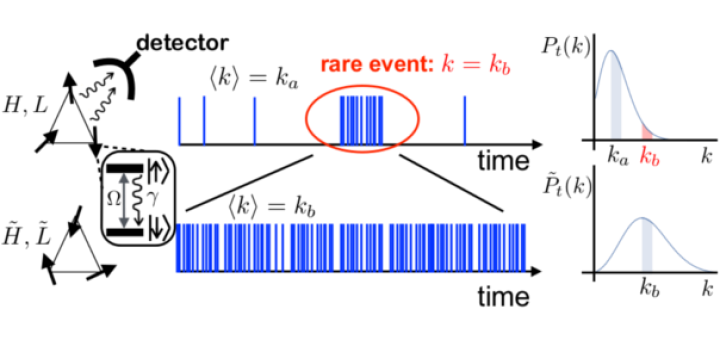
Theoretical Challenges in Levitated Nanomechanics: the case of magnon-phonon interaction
Title: Theoretical Challenges in Levitated Nanomechanics: the case of magnon-phonon interaction. When: Thursday, May 10, (2018), 15:00. Place: Department of Theoretical Condensed Matter Physics, Faculty of Sciences, Module 5, Seminar Room (5th Floor). Speaker:...